The given sequence is

The standard Explicit formula for an arithmetic sequence is given by

Where aₙ is the nth term, a₁ is the first term and d is the common difference
The common difference is basically the difference between any two consecutive terms
d = 26 - 20 = 6
d = 20 - 14 = 6
d = 14 - 8 = 6
d = 8 - 2 = 6
So the common difference is 6
The first term in the sequence is 2
So the Explicit formula for an arithmetic sequence becomes
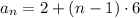
Now let us find the Recursive rule of this arithmetic sequence
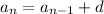
Where aₙ is the nth term, aₙ₋₁ is the previous term of the nth term, and d is the common difference
We already know the common difference is 6
So the Recursive rule for an arithmetic sequence becomes

Therefore, the RECURSIVE rule & EXPLICIT rules are
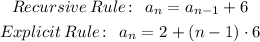
Let us simplify the above explicit rule
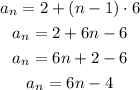
Therefore, the above explicit rule is also valid.