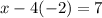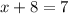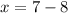Question

Solve this system by elimination : -5x + 3z =8 x- 4y = 7 5y - 4z = -14 find the x , y and z using elimination

Answer 1

• x = –1

• y = –2

• z = 1

Step-by-step explanation

Given the system:

`\begin{gathered} -5x+3z=8\text{, equation 1} \\ 5y-4z=-14,\text{ equation 2} \\ x-4y=7,\text{ equation 3} \end{gathered}`

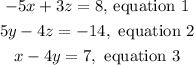
We have to divide equation 1 over 5 and add it to equation 2:

`\begin{gathered} -(5x)+0y+3z=8 \\ x-4y+0z=7 \\ 0x+5y-4z=-14 \end{gathered}`
`\begin{gathered} (-(5x)+0y+3z=8)/(5) \\ x-4y+0z=7 \\ 0x+5y-4z=-14 \end{gathered}`
`\begin{gathered} -x+0y+(3)/(5)z=(8)/(5) \\ x-4y+0z=7 \\ 0x+5y-4z=-14 \end{gathered}`

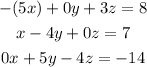
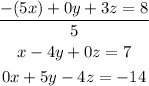
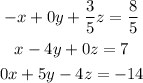
Now, we have to add 1/5(equation 1) to equation 2:

`\begin{gathered} -x+0y+(3)/(5)z=(8)/(5) \\ x-4y+0z=7 \\ --------- \\ 0x-4y+(3)/(5)z=(43)/(5) \end{gathered}`

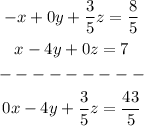
Next, we multiply the equation 2 obtained previously times 5:

`\begin{gathered} (0x-4y+(3)/(5)z=(43)/(5))\cdot5 \\ -20y+3z=43 \end{gathered}`

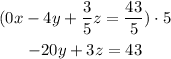
Then, we divide equation 2 over 4:

`\begin{gathered} (-20y+3z=43)/(4) \\ -5y+(3)/(4)z=(43)/(4) \end{gathered}`

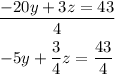
We add it to equation 3:

`\begin{gathered} -5y+(3)/(4)z=(43)/(4) \\ 5y-4z=-14 \\ ------- \\ 0y-(13)/(4)z=-(13)/(4) \end{gathered}`

Then, we are left with:

`\begin{equation*} -(13)/(4)z=-(13)/(4) \end{equation*}`

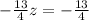
Simplifying:

`-13z=-13`
`z=(-13)/(-13)=1`
`z=1`

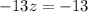
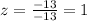
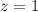
Now that we have the value of z (z = 1), we can replace it in the modified equation 2 and solve for y:

`-20y+3z=43`
`-20y+3(1)=43`
`-20y+3=43`
`-20y=43-3`
`-20y=40`
`y=(40)/(-20)`
`y=-2`

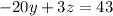
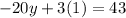
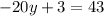
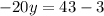
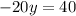
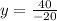
Finally, calculating the value of x with any of the equations (as we already have the other two values):

`x-4(-2)=7`
`x+8=7`
`x=7-8`
`x=-1`