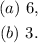When given a problem in which you have to choose subsets of length k from a set with n elements and:
1.- The order does not matter, you can use the number of combinations formula:
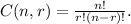
2.- The order matters, you can use the number of permutations formula:
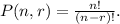
Therefore, using the first formula for part (b), and the second one for part (a) you get:
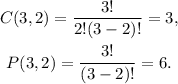
Answer: