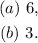Question

MO PROBABILITY AND STATISTICSIntroduction to permutations and combinationsSuppose we want to choose 2 letters, without replacement, from the 3 letters A, B, and C.(a) How many ways can this be done, if the order of the choices is relevant?(b) How many ways can this be done, if the order of the choices is not relevant?I need help with this math problem.

Answer 1

When given a problem in which you have to choose subsets of length k from a set with n elements and:

1.- The order does not matter, you can use the number of combinations formula:

`C(n,r)=(n!)/(r!(n-r)!).`

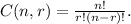
2.- The order matters, you can use the number of permutations formula:

`P(n,r)=(n!)/((n-r)!).`

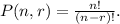
Therefore, using the first formula for part (b), and the second one for part (a) you get:

`\begin{gathered} C(3,2)=(3!)/(2!(3-2)!)=3, \\ P(3,2)=(3!)/((3-2)!)=6. \end{gathered}`

Answer:

`\begin{gathered} (a)\text{ 6,} \\ (b)\text{ 3.} \end{gathered}`