Question

In the figure below, A is a 44 N block and B is a 22 N block. (a) Determine the minimum weight (block C) that must be placed on A to keep it from sliding, if the coefficient of static friction between A and the table is 0.20. (b) Block C suddenly is lifted off A. Calculate the acceleration of block A, if the coefficient of kinetic friction between A and the table is 0.15.

Answer 1

Given data:

* The weight of the block A is 44 N.

* The weight of the block B is 22 N.

* The coefficient of static friction between A and table is 0.20.

Solution:

(a). The weight of the A and C block is balanced by the weight of the block B.

Thus, the friction force acting on the Block A in terms of the weight of the Block B is,

`W_B=\mu_sW_(AC)`

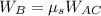
This describe the static friction force acting on the Block A ( with block C above it) in contact with the table.

where W_AC is the combined weight of block A and C, W_B is the weight of the block B, and

`\mu_s\text{ is the static friction}`

Substituting the known values,

`\begin{gathered} 22\text{ = }0.2* W_(AC) \\ W_(AC)=(22)/(0.2) \\ W_(AC)=110\text{ N} \end{gathered}`

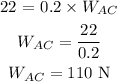
Thus, the minimum weight of the block C in terms of combined weight is,

`\begin{gathered} W_C=W_(AC)-W_A \\ W_C=110-44 \\ W_c=66\text{ N} \end{gathered}`

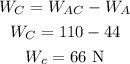
Hence, the minimum weight of the block C is 66 N.