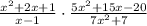Question

Drag each expression to the correct location on the model not all the expressions will be used

Answer 1

Given the expression:

`(5x^2+25x+20)/(7x)`

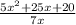
Let's determine where each piece belongs to create a rational expression equivalent to the expression given.

To determine, where each piece belong, let's input each value and simplify.

First simplify the given expression

`\begin{gathered} (5x^2+25x+20)/(7x) \\ \\ =(5(x+1)(x+4))/(7x) \end{gathered}`

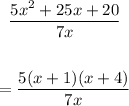
Thus, we have:

`(x^2+2x+1)/(x-1)\cdot(5x^2+15x-20)/(7x^2+7)`

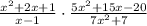
Let's simplify the expression above to verify if it is equivalent to the simplified expression of the given expression.

We have:

`\begin{gathered} (x^2+2x+1)/(x-1)\cdot(5x^2+15x-20)/(7x^2+7) \\ \\ =((x+1)^2)/(x-1)\cdot(5(x-1)(x+4))/(7x^2+7) \\ \\ =((x+1)^2)/(x-1)\cdot\frac{5(x-1)(x+4)}{7x(x^{}+1)} \\ \\ =((x+1))/(1)\cdot(5(x+4))/(7x) \\ \\ =(5(x+1)(x+4))/(7x) \end{gathered}`

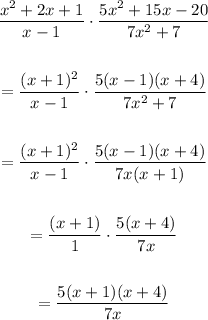
The expressions are equivalent.

Therefore, the correct expression is:

`(x^2+2x+1)/(x-1)\cdot(5x^2+15x-20)/(7x^2+7)`

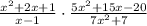
The expression in the numerator = 5x² + 15x - 20

The expression in the denominator = x - 1

ANSWER:

`(x^2+2x+1)/(x-1)\cdot(5x^2+15x-20)/(7x^2+7)`