The given problem can be exemplified in the following diagram:
Now we will add the torques with respect to the pivot. we will consider the torques counter-clockwise as positive. We get:
![\Sigma T=(80\operatorname{kg})(g)(d)-(5m-4.5m)(240\operatorname{kg})(g)]()
Since the system is still in equilibrium we will set the torques to zero:
![(80\operatorname{kg})(g)(d)-(5m-4.5m)(240\operatorname{kg})(g)=0]()
Now we solve the operations. We will use for the acceleration of gravity "g" the value of 9.8 m/s^2. We get:
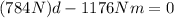
Now we solve for "d" first by adding 1176 to both sides:
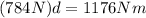
Now we divide both sides bt 784:
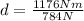
Solving the operations:
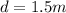
Therefore, the distance a person can walk is 1.5 meters.