Question

A plank of length L = 10 meters and mass 240 kg rests on the roof of a building and is set such that d = 4.5 meters of the plank is over the edge. A person of mass 80 kg slowly walks out onto the plank. How far past the edge of the building can the person walk on the plank without causing the plank to tip?

Answer 1

The given problem can be exemplified in the following diagram:

Now we will add the torques with respect to the pivot. we will consider the torques counter-clockwise as positive. We get:

Since the system is still in equilibrium we will set the torques to zero:

Now we solve the operations. We will use for the acceleration of gravity "g" the value of 9.8 m/s^2. We get:

`(784N)d-1176Nm=0`

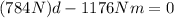
Now we solve for "d" first by adding 1176 to both sides:

`(784N)d=1176Nm`

Now we divide both sides bt 784:

`d=(1176Nm)/(784N)`

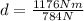
Solving the operations:

`d=1.5m`

Therefore, the distance a person can walk is 1.5 meters.