the equation:

has the form:
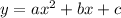
where a = 1, b = 18, and c= -12.
To complete the square, we need to add and subtract, the next term:
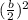
In this case:
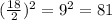
Adding and subtracting 81 to the parabola, we get:
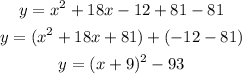
This equation has the form (the vertex form):
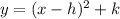
where (h,k) is the vertex of the parabola. Then, the turning point (vertex) is (-9, -93)