There are 50 dollar bills on the bag.
45 are one-dollar bills.
3 are five-dollar bills.
2 are ten-dollar bills.
If she takes one dollar bill on the bag, to determine the probability of each type of bill, you have to divide the number of bills of each type, by the total number of bills on the bag.
Then the probability of choosing one bill at random and taking a one-dollar bill can be calculated as follows:
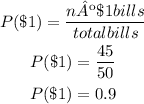
The probability of taking one five-dollar bill of the bag is:
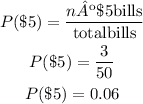
And the probability of taking a ten-dollar bill of the bag is:
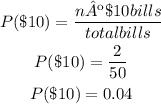
So the probability of choosing a one-dollar bill is 90%, which is likely, the probability of choosing a five-dollar bill is 6% and the probability of choosing a ten-dollar bill is 4%, both probabilities are very low, so it is unlikely that she will choose a five or a ten-dollar bill.