Question

Three ships, A, B, and C, are anchored in the atlantic ocean. The distance from A to B is 36.318 miles, from B to C is 37.674 miles, and from C to A is 11.164 miles. Find the angle measurements of the triangle formed by the three ships.A. m∠A=88.28267; m∠B=17.22942; m∠C=74.4879B. m∠A=74.4879; m∠B=17.22942; m∠C=88.28267C. m∠A=17.22942; m∠B=74.4879; m∠C=88.28267D. m∠A=88.28267; m∠B=74.4879; m∠C=17.22942

Answer 1

Question: Three ships, A, B, and C, are anchored in the Atlantic ocean. The distance from A to B is 36.318 miles, from B to C is 37.674 miles, and from C to A is 11.164 miles. Find the angle measurements of the triangle formed by the three ships.

Solution:

Note: In finding the angles of a triangle given its three sides, we will use the Cosine Law.

`\begin{gathered} c^2=a^2+b^2\text{ -2abcosC} \\ or\text{ it can be written as:} \\ \text{Cos(C) = }(a^2+b^2-c^2)/(2ab) \end{gathered}`

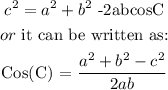
In finding angle C, we use the formula given above.

`\begin{gathered} \text{Cos(C) = }(37.674^2+11.164^2-36.318^2)/(2\cdot37.674\cdot11.164) \\ \text{Angle C = 74.4879 degrees} \end{gathered}`

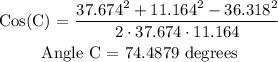
Note: Side a is the side opposite Angle A, side b is the side opposite Angle B, and side c is the side opposite Angle C.

Let's find the next angle.

`\begin{gathered} \text{Cos(B) = }(a^2+c^2-b^2)/(2ac) \\ \text{Cos(B) = }(37.647^2+36.318^2-11.164^2)/(2\cdot37.647\cdot36.318) \\ \text{Angle B = 17.2294}2\text{ degrees} \end{gathered}`

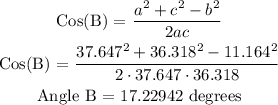
Note: We can still use the cosine law in finding Angle A. But another solution is subtracting the Angles A and B from 180 degrees. The measure of the internal angle of a triangle is always 180 degrees no matter what type of triangle it is.

`\begin{gathered} \text{Angle A = 180-74.4849 -17.22942} \\ \text{Angle A = 88.28 degrees} \end{gathered}`

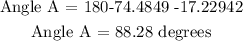
ANSWER:

A. m∠A=88.28267; m∠B=17.22942; m∠C=74.4879