Step 1: Write out the formula for binomial distribution
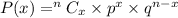
Where
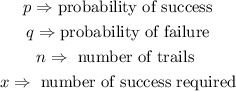
Step 2: State out the parameters needed in the formula to find the probabilty

Step 3: The probability that at most 2 children live with their father only can be described as;
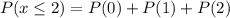
Step 4: Find the probability of each number of successes required
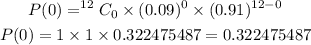
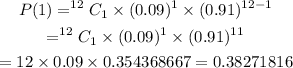

Step 5: Add all the number of successess required

Hence, the probability that at most 2 children live with their father only is 0.913