Question

A lab assistant needs to create a 1000 ML mixture that is 5% hydroelectric acid. The assistant has solutions of 3.5% and 6% in supply at the lab. Using the variables x and y to represent the number of milliliters of the 3.5% solution and the number of milliliters of the 6% solution respectively, determine a system of equation that describes the situation the situation.Enter the equations below separated by a comma How many milliliters of the 3.5% solution should be used?How many milliliters of 6% solution should be used?

Answer 1

Given:

A lab assistant needs to create a 1000 ML mixture that is 5% hydroelectric acid.

The assistant has solutions of 3.5% and 6% in supply at the lab.

let the number of milliliters from the solution of 3.5% = x

And the number of milliliters from the solution of 6% = y

so, we can write the following equations:

The first equation, the sum of the two solutions = 1000 ml

So, x + y = 1000

The second equation, the mixture has a concentration of 5%

so, 3.5x + 6y = 5 * 1000

So, the system of equations will be as follows:

`\begin{gathered} x+y=1000\rightarrow(1) \\ 3.5x+6y=5000\rightarrow(2) \end{gathered}`

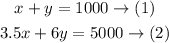
Now, we will find the solution to the system using the substitution method:

From equation (1)

`x=1000-y\rightarrow(3)`

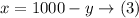
substitute with (x) from equation (3) into equation (2):

`3.5\cdot(1000-y)+6y=5000`

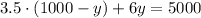
Solve the equation to find (y):

`\begin{gathered} 3500-3.5y+6y=5000 \\ -3.5y+6y=5000-3500 \\ 2.5y=1500 \\ y=(1500)/(2.5)=600 \end{gathered}`

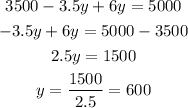
substitute with (y) into equation (3) to find x:

`x=1000-600=400`

So, the answer will be:

Enter the equations below separated by a comma

`x+y=1000,3.5x+6y=5000`

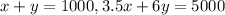
How many milliliters of the 3.5% solution should be used?

400 milliliters

How many milliliters of 6% solution should be used?

600 milliliters