Question

A person is at the top of a tower. He takes a segment of a string which measures 30 cm long when at rest and hooks his 3 kg sword at the end of it. The spring extends to 35 cm long. He will use this spring to get to the ground. What is the spring constant of the spring, and how much of the spring (measured at equibilirum) does he need in order to have a net force of 0 upon himself when he touches the ground? Assume he hangs the spring from a hook located exactly 30 m above the ground. Be certain to draw a free body diagram of the forces on him the moment he hits the ground.

Answer 1

The given problem can be exemplified in the following diagram:

To determine the constant of the spring we can use Hook's law, which is the following:

`F=k\Delta x`

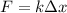
Where:

`\begin{gathered} F=\text{ force on the string} \\ k=\text{ string constant} \\ \Delta x=\text{ difference in length} \end{gathered}`

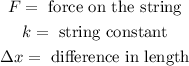
Now, we solve for "k" by dividing both sides by the difference in length:

`(F)/(\Delta x)=k`

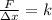
The force on the string is equivalent to the weight attached to it. The weight is given by:

`W=mg`

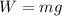
Where:

`\begin{gathered} W=\text{ weight} \\ m=\text{ mass} \\ g=\text{ acceleration of gravity} \end{gathered}`

Substituting in the formula for the constant of the spring we get:

`(mg)/(\Delta x)=k`

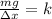
Now, we substitute the values:

Before solving we need to convert the centimeters into meters. To do that we use the following conversion factor:

Therefore, we get:

Substituting in the formula we get:

`((3kg)(9.8(m)/(s^2)))/(0.35m-0.30m)=k`

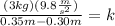
Solving the operations:

`588(N)/(m)=k`

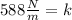
Therefore, the constant of the spring is 588 N/m.