Question

What are the roots of the equation ?-3x = -10x^2-4

Answer 1

Given the following Quadratic equation:

`-3x=-10x^2-4​`

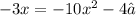
You can use the Quadratic formula to solve it:

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

In this case, you need to add "3x" to both sides of the equation:

`\begin{gathered} -3x+(3x)=-10x^2-4​+(3x) \\ 0=-10x^2+3x-4 \end{gathered}`

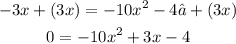
You can identify that:

`\begin{gathered} a=-10 \\ b=3 \\ c=-4 \end{gathered}`

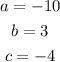
Substituting values into the formula and evaluating, you get:

`\begin{gathered} x=\frac{-3\pm\sqrt[]{3^2^{}-4(-10)(-4)}}{2(-10)} \\ \\ x_1=(3)/(20)-(i)/(20)\sqrt[]{151} \\ \\ x_2=(3)/(20)+(i)/(20)\sqrt[]{151} \end{gathered}`

Answer

Complex roots:

`\begin{gathered} x_1=(3)/(20)-(i)/(20)\sqrt[]{151} \\ \\ x_2=(3)/(20)+(i)/(20)\sqrt[]{151} \end{gathered}`