We are given the graph of a line and we are asked to determine its equation in point-slope form.
The general form in slope point form of a line is:
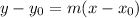
Where:
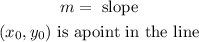
to determine the slope we will use the following formula:

Where:
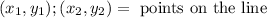
We will choose two points on the line from the graph:
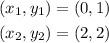
Now, we plug in the values in the formula for the slope:
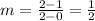
Now, we substitute the value of the slope in the equation of the line:
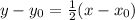
Now, we plug in the first point we choose for the line:
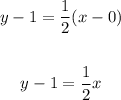
And thus we have determined the equation of the line in point-slope form.
The slope-intercept form is the following:

To convert this equation to slope-intercept form, we will take the previous equations and we will add 1 to both sides:
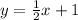
And thus we have determined the slope-intercept form of the equations of the line.