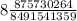Question

([20 + 10.4^2 - 116,870) / (20/ 1/3 x 15 - 10.4/ (116,870/6808))] ^-1

Answer 1

`8(875730264)/(8491541359)`

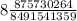
Explanation:

Given the values of the variables below:

• D = 116,870

,

• E=1/3

,

• L =15

,

• M = 20

,

• O = 10.4

,

• Y = 6,808

We are required to evaluate:

`\begin{gathered} \lbrack(M+O^2-D/ Y)/(M/ E\cdot L-O/(D/ Y))\rbrack^(-1) \\ =\mleft(((M+O^2-D/ Y))/((M/ E\cdot L-O/(D/ Y)))\mright)^(-1) \end{gathered}`

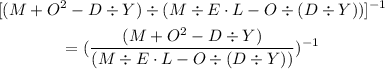
Substitute the given values:

`=\mleft((20+10.4^2-116,870/6,808)/(20/(1)/(3)\cdot15-10.4/(116,870/6,808))\mright)^(-1)`

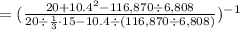
We simplify using the order of operations PEMDAS.

First, evaluate the parentheses in the denominator.

`=\mleft((20+10.4^2-116,870/6,808)/(20/(1)/(3)\cdot15-10.4/(116,870)/(6,808))\mright)^(-1)`

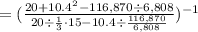
Next, evaluate the exponent(E): 10.4²

`=\mleft((20+108.16-116,870/6,808)/(20/(1)/(3)\cdot15-10.4/(116,870)/(6,808))\mright)^(-1)`

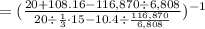
Next, we take multiplication and division together:

`\begin{gathered} =\mleft((20+108.16-(116,870)/(6,808))/(20*3*15-10.4*(6808)/(116,870))\mright)^(-1) \\ =\mleft((20+108.16-(116,870)/(6,808))/(900-(13616)/(22475))\mright)^(-1) \end{gathered}`

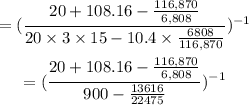
Finally, take addition and subtraction and then simplify.

`\begin{gathered} =\mleft((9445541)/(85100)/(20213884)/(22475)\mright)^(-1) \\ =((9445541)/(85100)*(22475)/(20213884))^(-1) \\ =((8491541359)/(68808061136))^(-1) \\ =1/(8491541359)/(68808061136)=1*(68808061136)/(8491541359) \\ \\ =(68808061136)/(8491541359) \\ =8(875730264)/(8491541359) \end{gathered}`

The result of the evaluation is:

`8(875730264)/(8491541359)`