Question

In science class, the students were asked to create a container to hold an egg they would then drop this container from a window that is 25 feet above the ground if the equation of the containers pathway can be modelled by the equation: H =-16t²+25Find is the maximum height of the container?

Answer 1

25 feet

Step-by-step explanation:

The equation that models the pathway of the container is:

`h=-16t^2+25`

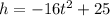
The maximum height occurs at the axis of symmetry.

First, we find the equation of symmetry:

`\begin{gathered} x=-(b)/(2a)where\begin{cases}a=-16 \\ b=0\end{cases} \\ x=-(0)/(2*-16) \\ x=0 \\ \implies t=0 \end{gathered}`

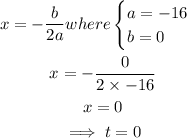
Next, determine the value of h at t=0.

`\begin{gathered} h=-16(0)^2+25 \\ h=25\text{ feet} \end{gathered}`

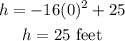
The maximum height of the container is 25 feet.