Answer:
25 feet
Step-by-step explanation:
The equation that models the pathway of the container is:
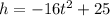
The maximum height occurs at the axis of symmetry.
First, we find the equation of symmetry:
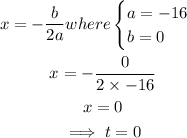
Next, determine the value of h at t=0.
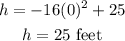
The maximum height of the container is 25 feet.