ANSWER:
a) 83,000 people
b) 122,860 people
c) 4.75 years
Explanation:
We have that the population given by the following equation:
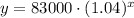
a) What was the population in 2010?
Since no year has passed, the value of x would be 0.
Replacing:
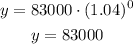
The population in 2010 is 83,000 people
b) What is the population in 2020?
From 2010 to 2020 10 years have passed, therefore the value of x is 10
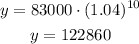
The population in 2020 is 122,860 people
c) When will the population reach 100,000?
Since the population is 100,000 people, it is the value of y, therefore we must solve and calculate the value of x
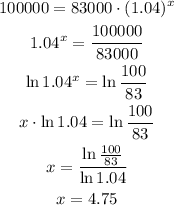
Which means that for the population to be 100,000 people, 4.75 years would have to pass