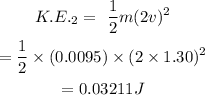Given that mass of bullet, m = 9.50 g = 0.0095 kg
speed of bullet, v is 1.30 km/s
(a) Kinetic energy is given by the formula
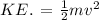
Substituting the values in the above formula, we get
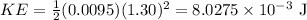
(b) Speed of bullet is v/2
Sustituting this value in the formula of kinetic energy, we get
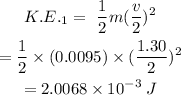
(c) Speed of bulllet becomes 2v
Sustituting this value in the formula of kinetic energy, we get