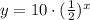Question

Decide whether the word problem represents a linear or exponential function. Circle either linear or exponential. Then, write the function formula.

Answer 1

a. The given table is

Notice, the value of x increases at equal intervals of 1

Also, the value of y increases at an equal interval of 3

This means for the y values the difference between consecutive terms is 3

Also, for the x values, the difference between consecutive terms is 1

Hence, the table represents a linear function

The general form of a linear function is

`y=mx+c`

Where m is the slope

From the interval increase

`m=(\Delta y)/(\Delta x)=(3)/(1)=3`

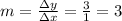
Hence, m = 3

The equation becomes

`y=3x+c`

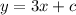
To get c, consider the values

x = 0 and y = 2

Thi implies

`\begin{gathered} 2=3(0)+c \\ c=2 \end{gathered}`

Hence, the equation of the linear function is

`y=3x+2`

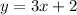
b. The given table is

Following the same procedure as in (a), it can be seen that there is no constant increase in the values of y

Hence, the function is not linear

This implies that the function is exponential

The general form of an exponential function is given as

`y=a\cdot b^x`

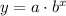
Consider the values

x =0, y = 3

Substitute x = 0, y = 3 into the equation

This gives

`\begin{gathered} 3=a* b^0 \\ \Rightarrow a=3 \end{gathered}`

The equation become

`y=3\cdot b^x`

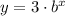
Consider the values

x =1, y = 6

Substitute x = 1, y = 6 into the equation

This gives

`\begin{gathered} 6=3\cdot b^1 \\ \Rightarrow b=(6)/(3)=2 \end{gathered}`

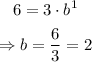
Therefore the equation of the exponential function is

`y=3\cdot2^x`

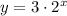
c. The given table is

As with (b) above,

The function is exponential

Using

`y=a\cdot b^x`

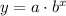
When

x = 0, y = 10

This implies

`\begin{gathered} 10=a\cdot b^0 \\ \Rightarrow a=10 \end{gathered}`

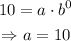
The equation becomes

`y=10\cdot b^x`

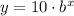
Also, when

x = 1, y =5

The equation becomes

`\begin{gathered} 5=10\cdot b^1 \\ \Rightarrow b=(5)/(10) \\ b=(1)/(2) \end{gathered}`

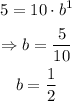
Therefore, the equation of the exponential function is

`y=10\cdot((1)/(2))^x`