Question

Two figures are similar. The smaller figure has dimensions that are 3:4 the size of the largerfigure. If the area of the larger figure is 100 square units, what is the area of the smallerfigure?

Answer 1

56.25

Explanation:

We are told that the side lengths of the smaller figure are 3/4 the length of the larger figure.

`S_(small)=(3)/(4)* S_(large)`

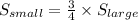
Now since the area is proportional to the equal of the side lengths, we have

`A_(small)=S_(small)^2^`
`A_(small)=((3)/(4))^2* S_(large)^2`
`=A_(small)=((3)/(4))^2* A_(large)^2`

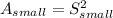
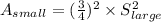
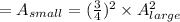
The last is true since A_large = S^2_large.

Now we are told that A_large = 100 square units; therefore,

`A_(small)=((3)/(4))^2*100`
`\Rightarrow A_(small)=(9)/(16)*100`

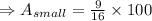
which we evaluate to get

`A_(small)=(9)/(16)*100=56.25`
`\boxed{A_(small)=56.25.}`

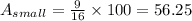
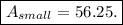
Hence, the area of the smaller figure is 56.25.