4.8 mi
Step-by-step explanation
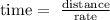
Step 1
Set the equations
a) uphill
let
rate1= 1.5 miles per hour
time= unknow= t1
distance = x
b) down hille
rate=4 miles per hour
time=time2=one hour less than the time to climb = t1-1
distance = x
so
replacing

Step 2
solve the equations
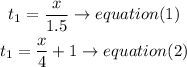
set t1= t1
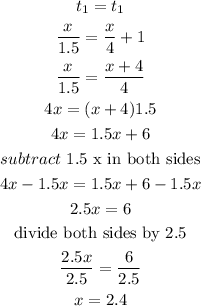
it means the distance to the top of the mountain is 2.4 miles, so the entire hike is twice that amount
total distance=2.4 mi*2
total distance=4.8 miles
Step 3
now, the times
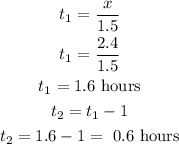
table
I hope this helps you