Question

If the time to climb the mountain took an hour more than the time to hike down how long was entire hike?

Answer 1

4.8 mi

Step-by-step explanation

`\text{time}=\text{ }\frac{\text{distance}}{\text{rate}}`

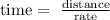
Step 1

Set the equations

a) uphill

let

rate1= 1.5 miles per hour

time= unknow= t1

distance = x

b) down hille

rate=4 miles per hour

time=time2=one hour less than the time to climb = t1-1

distance = x

so

replacing

`\begin{gathered} t_1=\frac{x}{1.5\frac{mi}{\text{hour}}}\rightarrow t_1=(x)/(1.5)\rightarrow equation(1) \\ t_2=\frac{x}{4\frac{mi}{\text{hour}}} \\ \text{replace t}_2=t_1-1 \\ t_1-1=(x)/(4) \\ \text{add 1 in both sides} \\ t_1-1+1=(x)/(4)+1 \\ t_1=(x)/(4)+1\rightarrow equation(2) \end{gathered}`

Step 2

solve the equations

`\begin{gathered} t_1=(x)/(1.5)\rightarrow equation(1) \\ t_1=(x)/(4)+1\rightarrow equation(2) \end{gathered}`

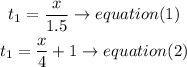
set t1= t1

`\begin{gathered} t_1=t_1 \\ (x)/(1.5)=(x)/(4)+1 \\ (x)/(1.5)=(x+4)/(4) \\ 4x=(x+4)1.5 \\ 4x=1.5x+6 \\ subtract\text{ 1.5 x in both sides} \\ 4x-1.5x=1.5x+6-1.5x \\ 2.5x=6 \\ \text{divide both sides by 2.5} \\ (2.5x)/(2.5)=(6)/(2.5) \\ x=2.4 \end{gathered}`

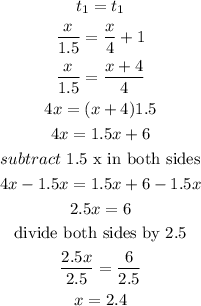
it means the distance to the top of the mountain is 2.4 miles, so the entire hike is twice that amount

total distance=2.4 mi*2

total distance=4.8 miles

Step 3

now, the times

`\begin{gathered} t_1=(x)/(1.5) \\ t_1=(2.4)/(1.5) \\ t_1=1.6\text{ hours} \\ t_2=t_1-1 \\ t_2=1.6-1=\text{ 0.6 hours} \end{gathered}`

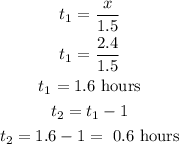
table

I hope this helps you