We have to calculate the area and perimeter of ABC.
Area:
We can calculate the area by substracting from the area of the big triangle ABD the area of the little triangle BCD. Both are right triangles.
The area of ABD is:
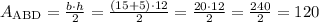
The area of BCD is:
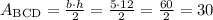
Then, the area of ABC is:
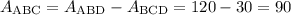
The area of ABC is 90 cm^2.
Perimeter:
We calculate the perimeter by adding the length of the three sides. We know only 2 of the sides, so we have to calculate the other one (BC).
The length of BC can be calculated using Pythagorean theorem for the triangle BCD, so we can write:
![\begin{gathered} BC^2=CD^2+BD^2=5^2+12^2=25+144=169 \\ BC=\sqrt[]{169}=13 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/ffh0s89iz49xz4ggu3edmwqgowhbk945ol.png)
Now, we can calculate the perimeter as:
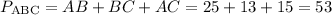
The perimeter is 53 cm.