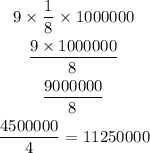Question

(9 •10^9)•(2•10)^-3)

Answer 1

First, let's distribute the exponent -3 for 2 and ten, like this:

`\begin{gathered} 9*10^9*(2*10)^(-3)^{} \\ 9*10^9*2^(-3)*10^(-3) \end{gathered}`

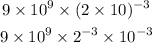
Now, we can apply the next property when we have a number raised to a negative power:

`a^(-b)=(1)/(a^b)`

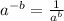
Then:

`\begin{gathered} 9*10^9*2^(-3)*(1)/(10^3) \\ 9*2^(-3)*(10^9)/(10^3) \end{gathered}`

And when we have a division of the same number raised to different powers we can apply:

`(a^b)/(a^c)=a^(b-c)`

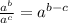
then:

`\begin{gathered} 9*2^(-3)*(10^9)/(10^3) \\ 9*2^(-3)*10^(9-3) \\ 9*2^(-3)*10^6 \\ 9*(1)/(2^3)^{}*10^6 \end{gathered}`

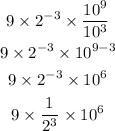
Now, as we know, having 10 raised to 6 means that we are multiplying ten by ten 6 times, when we do this we get:

`10*10*10*10*10*10=1000000`

And with 2 raised to three we get:

`2*2*2=8`

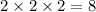
Then we have:

`\begin{gathered} 9*\frac{1}{8^{}}^{}*1000000 \\ \frac{9*1000000}{8^{}}^{} \\ \frac{9000000}{8^{}}^{} \\ (4500000)/(4)^{}=11250000 \end{gathered}`