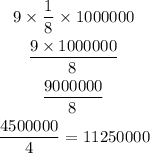First, let's distribute the exponent -3 for 2 and ten, like this:
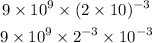
Now, we can apply the next property when we have a number raised to a negative power:
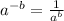
Then:
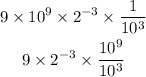
And when we have a division of the same number raised to different powers we can apply:
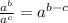
then:
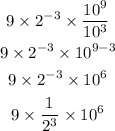
Now, as we know, having 10 raised to 6 means that we are multiplying ten by ten 6 times, when we do this we get:
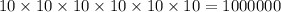
And with 2 raised to three we get:
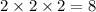
Then we have: