To answer this question, we need to apply the following rule:

This rule is known as the negative exponent rule. We also need to remember that when we have an exponent of 1/2 is the same as finding the square root for a number. Then, we have:
![((1)/(4))^{-(1)/(2)}=\frac{1}{((1)/(4))^{(1)/(2)}}=\frac{1}{\frac{\sqrt[]{1}^{}}{\sqrt[]{4}}}](https://img.qammunity.org/2023/formulas/mathematics/college/d51rvvyp5828n9y4mzblk3hhol1gmk8xnl.png)
Therefore, we have:
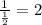
Thus, we have that:
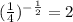
In summary, the correct answer is 2 (second option).