Question

4 Evaluate: 2 (1) - O 1 16 2 ( ) V2 O O 1 2

Answer 1

To answer this question, we need to apply the following rule:

`x^(-m)=(1)/(x^m)`

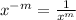
This rule is known as the negative exponent rule. We also need to remember that when we have an exponent of 1/2 is the same as finding the square root for a number. Then, we have:

`((1)/(4))^{-(1)/(2)}=\frac{1}{((1)/(4))^{(1)/(2)}}=\frac{1}{\frac{\sqrt[]{1}^{}}{\sqrt[]{4}}}`

Therefore, we have:

`(1)/((1)/(2))=2`

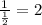
Thus, we have that:

`((1)/(4))^{-(1)/(2)}=2`

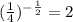
In summary, the correct answer is 2 (second option).