Question

I need help with problem 7.Use the figure to find the values of x, y, and z that makes triangle DEF similar to triangle GHF.

Answer 1

• x = 12

,

• y = 16

,

• z = 7

Step-by-step explanation

Because the triangles are similar, we have that:

• The ratio between corresponding sides is constant:

`(DE)/(GH)=(EF)/(GF)=(DF)/(HF)`

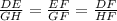
• Corresponding angles are congruent:

`\begin{gathered} \angle D\cong\angle H \\ \angle E\cong\angle G \\ \angle F\cong\angle F \end{gathered}`

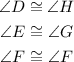
We know that the measure of angle E is 16°, so the measure of angle G must be the same because they are congruent,

`16\degree=2(x-4)\degree`

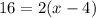
With this equation, we can find x. First, divide both sides by 2,

`\begin{gathered} (16)/(2)=(2(x-4))/(2) \\ \\ 8=x-4 \end{gathered}`

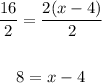
And then, add 4 to both sides,

`\begin{gathered} 8+4=x-4+4 \\ \\ 12=x \end{gathered}`

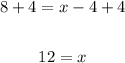
Hence, x = 12.

Now we know that the length of side EF is,

`EF=x-5=12-5=7`

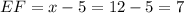
To find y and z, we will use the proportions we got at the top of this explanation,

`(DE)/(GH)=(EF)/(GF)=(DF)/(HF)`

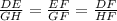
Replace with the known values and the expressions with y and z,

`(25)/(6z+8)=(7)/(14)=(24)/(3y)`

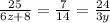
With the first two, we can find z,

`(25)/(6z+8)=(7)/(14)`

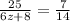
Simplify the right side,

`(25)/(6z+8)=(1)/(2)`

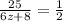
Rise both sides to the exponent -1 - i.e. flip both sides of the equation,

`(6z+8)/(25)=2`

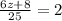
Multiply both sides by 25,

`\begin{gathered} 25\cdot((6z+8))/(25)=2\cdot25 \\ \\ 6z+8=50 \end{gathered}`

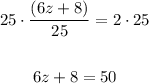
Subtract 8 from both sides,

`\begin{gathered} 6z+8-8=50-8 \\ 6z=42 \end{gathered}`

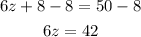
And divide both sides by 6,

`\begin{gathered} (6z)/(6)=(42)/(6) \\ \\ z=7 \end{gathered}`

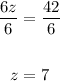
Hence, z = 7.

Finally, with the last two proportions, we can find y,

`(7)/(14)=(24)/(3y)`

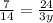
The first two steps are the same we did to find z: simplify the left side and flip both sides,

`2=(3y)/(24)`

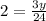
Multiply both sides by 24,

`\begin{gathered} 24\cdot2=24\cdot(3y)/(24) \\ \\ 48=3y \end{gathered}`

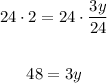
And divide both sides by 3,

`\begin{gathered} (48)/(3)=(3y)/(3) \\ \\ 16=y \end{gathered}`

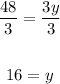
Hence, y = 16.