ANSWER
• x = 12
,
• y = 16
,
• z = 7
Step-by-step explanation
Because the triangles are similar, we have that:
• The ratio between corresponding sides is constant:
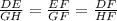
• Corresponding angles are congruent:
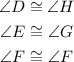
We know that the measure of angle E is 16°, so the measure of angle G must be the same because they are congruent,

With this equation, we can find x. First, divide both sides by 2,

And then, add 4 to both sides,
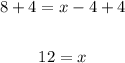
Hence, x = 12.
Now we know that the length of side EF is,
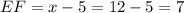
To find y and z, we will use the proportions we got at the top of this explanation,
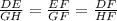
Replace with the known values and the expressions with y and z,
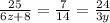
With the first two, we can find z,
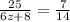
Simplify the right side,
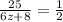
Rise both sides to the exponent -1 - i.e. flip both sides of the equation,
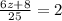
Multiply both sides by 25,
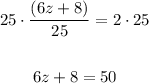
Subtract 8 from both sides,
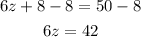
And divide both sides by 6,
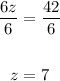
Hence, z = 7.
Finally, with the last two proportions, we can find y,
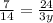
The first two steps are the same we did to find z: simplify the left side and flip both sides,
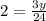
Multiply both sides by 24,
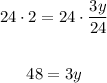
And divide both sides by 3,
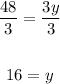
Hence, y = 16.