Question

Allison earned a score of 150 on Exam A that had a mean of 100 and a standard deviation of 25. She is about to take Exam B that has a mean of 200 and a standard deviation of 40. How well must Allison score on Exam B in order to do equivalently well as she did on Exam A? Assume that scores on each exam are normally distributed.

Answer 1

Answer:

Allison must score 280 on Exam B to do equivalently well as she did on Exam A

Explanations:

Note that:

`\begin{gathered} z-\text{score = }(x-\mu)/(\sigma) \\ \text{where }\mu\text{ represents the mean} \\ \sigma\text{ represents the standard deviation} \end{gathered}`
`\begin{gathered} \text{For Exam A:} \\ x\text{ = 150} \\ \mu\text{ = 100} \\ \sigma\text{ = 25} \\ z-\text{score = }(150-100)/(25) \\ z-\text{score = 2} \end{gathered}`

Since we want Allison to perform similarly in Exam A and Exam B, their z-scores will be the same

Therefore for exam B:

`\begin{gathered} \mu\text{ = 200} \\ \sigma\text{ = 40} \\ z-\text{score = 2} \\ z-\text{score = }(x-\mu)/(\sigma) \\ 2\text{ = }(x-200)/(40) \\ 2(40)\text{ = x - 200} \\ 80\text{ = x - 200} \\ 80\text{ + 200 = x} \\ x\text{ = 280} \end{gathered}`

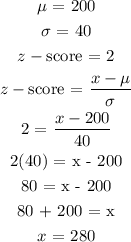
Allison must score 280 on Exam B to do equivalently well as she did on Exam A