Answer:
Allison must score 280 on Exam B to do equivalently well as she did on Exam A
Explanations:
Note that:


Since we want Allison to perform similarly in Exam A and Exam B, their z-scores will be the same
Therefore for exam B:
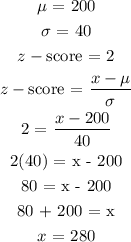
Allison must score 280 on Exam B to do equivalently well as she did on Exam A