Question

If Tanisha wants the top of the ladder to reach exactly 8 feet up the building, what is X, the distance between the building and the base of the ladder in feet?

Answer 1

Given:

The right triangle can be sketched as shown below;

To get the distance between the building and the base of the ladder, we use the Pythagoras theorem since it is a right triangle.

`\begin{gathered} \text{hypotenuse}^2=\text{adjacent}^2+\text{opposite}^2 \\ \\ \text{where;} \\ \text{hypotenuse}=10 \\ \text{adjacent}=x \\ \text{opposite}=8 \end{gathered}`

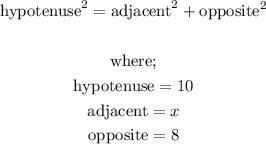
Hence,

`\begin{gathered} \text{hypotenuse}^2=\text{adjacent}^2+\text{opposite}^2 \\ 10^2=x^2+8^2 \\ 100=x^2+64 \\ 100-64=x^2 \\ 36=x^2 \\ x=\sqrt[]{36} \\ x=6 \end{gathered}`

Therefore, the distance between the building and the base of the ladder in feet is 6 feet.