The circumference of a circle is given by the following formula
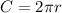
where r represents the radius.
The ratio between two circumferences is equal to the ratio of the radius.
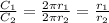
The area of a circle is given by the following formula
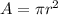
Then, the ratio between two circle areas is equal to the square of the ratio of the radius, which is the square of the ratio between the circumferences.
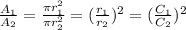
Then, applying this relation in our problem, the ratio between the areas is:
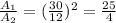
The ratio between the areas is 25/4.