Question

3. You draw one card from a standard deck.(a) What is the probability of selecting a king or a queen? (b) What is the probability of selecting a face card or a 10? (c) What is the probability of selecting a spade or a heart? (d) What is the probability of selecting a red card or a black card?

Answer 1

Given:

The objective is to find,

a) The probability of selecting a king or a queen.

b) The probability of selecting a face card or a 10.

Step-by-step explanation:

The total number of cards in a deck is, N = 52 cards.

a)

Out of 52 cards, the number of king cards is,

`n(k)=4`

Similarly, out of 52 cards, the number of queen cards is,

`n(q)=4`

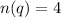
Then, the probability of drawing one out of 4 king cards or one out of 4 queen cards can be calculated as,

`\begin{gathered} P(E)=P(k)+P(q) \\ =(n(k))/(N)+(n(q))/(N) \\ =(4)/(52)+(4)/(52) \\ =(8)/(52) \end{gathered}`

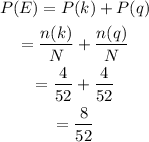
Hence, the probsability of selecting a king or a queen is (8/52).

b)

Out of 52 cards, the number of face cards is 12.

`n(f)=12`

Similarly, out of 52 cards, the number of 10 is,

`n(10)=4`

Then, the probability of drawing one out of 12 face cards or one out of 4 ten cards can be calculated as,

`\begin{gathered} P(E)=P(f)+P(10) \\ =(12)/(52)+(4)/(52) \\ =(12+4)/(52) \\ =(16)/(52) \end{gathered}`

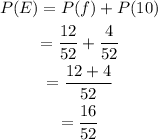
Hence, the probability of selecting a face card or a 10 is (16/52).

c)

Out of 52 cards, the number of spade cards is 13.

`n(s)=13`

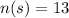
Similarly, out of 52 cards, the number of heart cards is 13.

`n(h)=13`

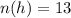
Then, the probability of drawing one out of 13 spade cards or one out of 13 heart cards can be calculated as,

`\begin{gathered} P(E)=P(s)+P(h) \\ =(n(s))/(N)+(n(h))/(N) \\ =(13)/(52)+(13)/(52) \\ =(26)/(52) \end{gathered}`

Hence, the probability of selecting a spade or a heart is 26/52.

d)

Out of 52 cards, the number of red cards is,

`n(r)=26`

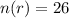
Out of 52 cards, the number of black cards is,

`n(b)=26`

Then, the probability of drawing one out of 26 red cards or one out of 26 black cards is,

`\begin{gathered} P(E)=P(r)+P(b) \\ =(n(r))/(N)+(n(b))/(N) \\ =(26)/(52)+(26)/(52) \\ =(52)/(52) \\ =1 \end{gathered}`

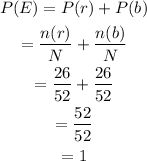
Hence, the probability of selecting a red card or a black card is 1.