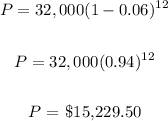Question

A car that originally valued at $32,000 loses 18% of its value every 3 years. What will be the value of the car after 12 years?

Answer 1

The value of the car after 12 years is $15,229.50

Here, we want to calculate the value of a car that loses a percentage of its origial value after some years

To do this, we shall need an exponential equation that represents decay or depreciation

We can have this as;

`P=I(1-r)^t`

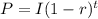
where;

P is the present value that we want to calculate

I represents the original value of the car which is $32,000

r is the percentage of decrease per year

From the question, there is a decrease of 18% every 3 years

The percentage decrease per year will be 18%/3 = 6%

6% is same as 6/100 = 0.06

t represents the time frame we are considering = 12 years

We proceed to input all these values into the equation above

We have it as;

`\begin{gathered} P=32,000(1-0.06)^(12) \\ \\ P=32,000(0.94)^(12) \\ \\ P\text{ = \$15,229.50} \end{gathered}`