Question

h(r) = (r +1)(r+8)1) What are the zeros of the function?Write the smaller r first, and the larger second.smaller r =larger s 2) What is the vertex of the parabola

Answer 1

For the zeros of the function, we have to solve h(r)=0, therefore:

`\begin{gathered} h(r)=(r+1)(r+8) \\ h(r)=0 \\ \Rightarrow(r+1)(r+8)=0 \\ \Rightarrow r=-1\text{ or } \\ r=-8 \end{gathered}`

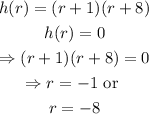
then, the smaller r is -8 and the larger is -1.

Now, to find the vertex of the parabola, we can find the x-coordinate of the vertex from the general rule:

`\begin{gathered} f(x)=ax^2+bx+c \\ \text{ x-coordinate: -b/2a} \end{gathered}`

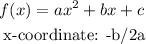
In this case, we have the following:

`\begin{gathered} h(r)=(r+1)(r+8)=r^2+8r+r+8=r^2+9r+8 \\ \Rightarrow a=1,b=9 \\ \Rightarrow-(b)/(2a)=-(9)/(2(1))=-(9)/(2) \end{gathered}`

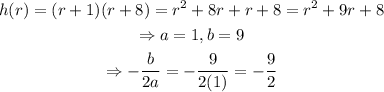
now that we have the x-coordinate of the vertex, we just evaluate the function on that point to find the y-coordinate of the vertex:

`h(-(9)/(2))=(-(9)/(2)+1)(-(9)/(2)+8)=(-(7)/(2))((7)/(2))=-(49)/(4)`

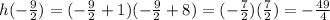
therefore, the vertex of the parabola is the point (-9/2,-49/4)