For the zeros of the function, we have to solve h(r)=0, therefore:
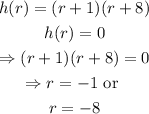
then, the smaller r is -8 and the larger is -1.
Now, to find the vertex of the parabola, we can find the x-coordinate of the vertex from the general rule:
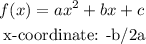
In this case, we have the following:
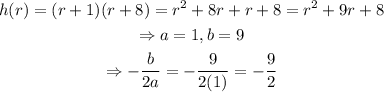
now that we have the x-coordinate of the vertex, we just evaluate the function on that point to find the y-coordinate of the vertex:
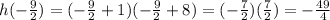
therefore, the vertex of the parabola is the point (-9/2,-49/4)