Question

Jan plans to tell two people each day and will ask that person to tell two other people each day through the day of the opening, and so on. Assume that each new person who hears about the soft opening is also asked to tell two other people each day through the day of the opening and that each one starts the process of telling their friends on the day after he or she first hears. When should Jan begin telling others about the soft opening in order to have at least 700 people know about it by the day it occurs?

Answer 1

Step-by-step explanation:

From the given question, we can sketch the pattern observed

The figure above helps show how the number of people increases

Initially, Jan tells 2 more people, then the two people tell two more people, then they also tell two more people

Thus

we can see that the model is given by

`\begin{gathered} (2)^n \\ where\text{ n is the number of days} \end{gathered}`

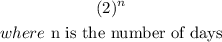
In order to have at least 700 (it also means a minimum of 700), we will have the equation

`2^n\ge700`

We then solve for n

Taking the log of both sides

`n\text{ }log2\ge log700`
`n\ge(log700)/(log2)`

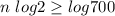
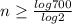
So that

`\begin{gathered} n\ge(2.845)/(0.301) \\ \\ n\ge9.451 \end{gathered}`

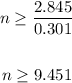
So, the number of days will be at least 10 days (Rounded to the nearest whole day )