Question

Four more than three times a number, is less than 30. Which of the following is not a solution?61278

Answer 1

- To solve the question, we simply need to interpret the question line by line.

- Let the number be x.

- "Four more than three times a number" can be written as:

`\begin{gathered} \text{ Three times a number is: }3x \\ \text{ For more than three times a number becomes: }4+3x \end{gathered}`

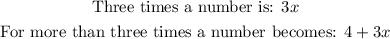
- "Four more than three times a number is less than 30" can be written as:

`4+3x<30`

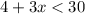
- Now, we can proceed to solve the inequality and find the appropriate range of x. This is done below:

`\begin{gathered} 4+3x<30 \\ \text{ Subtract 4 from both sides} \\ 3x<30-4 \\ 3x<26 \\ \text{ Divide both sides by 3} \\ (3x)/(3)<(26)/(3) \\ \\ \therefore x<8(2)/(3) \end{gathered}`

- This means that all correct solutions to the inequality lie below 8.666...

- This further implies that any number greater than this is not part of the solutions of the inequality.

- 12 is greater than 8.666

Final Answer

The answer is 12