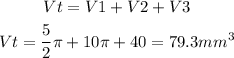The volume will be given by:
The volume of the half cylinder on top, plus the volume of the rectangular prims, plus the volume of the half cylinder on the right:
so:
The volume of the half cylinder on top is:
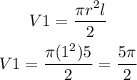
The volume of the half cylinder on the right is:
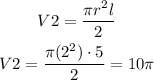
The volume of the rectangular prism is:
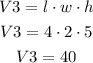
Therefore, the total volume is: