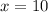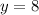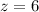Step-by-step explanation:
Consider the following problem.
A student library has 24 tables, X tables with 4 seats each, Y tables with 6 seats each, and Z tables with 10 seats each. The total seating capacity of the cafeteria is 148. For a special student academic meeting, half of the X tables, 1/4 of the Y tables, and 1/3 of the Z tables will be used, for a total of 9 tables. Determine X, Y, and Z.
The conditions of this problem give rise to the following system of equations
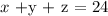
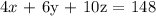
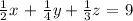
Multiplying the second equation by 1/2 and the third equation by 12, we get:
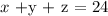

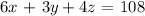
Now, multiply the first equation by -2 and add it to the second equation. In this way we obtain:
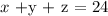
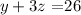
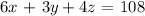
Multiply the first equation by -6 and add it to the last equation. In this way we obtain:
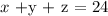
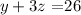
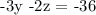
Finally, the process is completed by adding the second multiplied by 3 to the third equation.
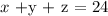
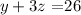
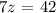
then, if we perform back substitution we get the desired solutions:
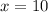
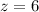
and
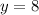
We can conclude that the correct answer is:
Answer:
Problem:
A student cafeteria has 24 tables, X tables with 4 seats each, Y tables with 6 seats each, and Z tables with 10 seats each. The total seating capacity of the cafeteria is 148. For a special student meeting, half of the X tables, 1/4 of the Y tables, and 1/3 of the Z tables will be used, for a total of 9 tables. Determine X, Y, and Z.
System of equations:
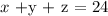
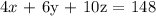
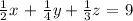
Solution for this system of equations: