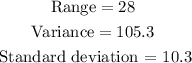Question

Find the range, the standard deviation, and the variance for the given samples. Round non-integer results to the nearest tenth.−10, −16, −21, −24, −4, −30, −32 range ________standard deviation __________variance __________

Answer 1

From the given values, we can see that the lowest values is -32 and the highest value ie -4. Since the range is the difference betwwwn the highest and the lowest value, the range is

`\begin{gathered} \text{Range}=-4-(-32) \\ \text{Range}=28 \end{gathered}`

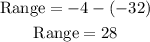
On the other hand, the sample variance formula is

`S^2=\sqrt[]{\frac{\sum ^7_(n\mathop=1)(x-\bar{x})^2}{n-1}}`

where x^bar is the mean and n is the total number of sample elements. In our case, n=7 and the mean is

`\begin{gathered} \bar{x}=(-10-16-21-24-4-30-32)/(7) \\ \bar{x}=-(137)/(7) \\ \bar{x}=-19.5714 \end{gathered}`

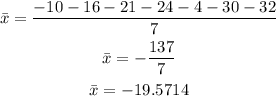
Then, the sample variance is given by

`\begin{gathered} S^2=((-10-19.57)^2+(-16-19.57)^2+(-21-19.57)^2+\cdot\cdot\cdot+(-32-19.57)^2)/(6) \\ S^2=105.2857 \end{gathered}`

Since the standard deviation is the square root of the sample variance, we have

`\begin{gathered} S=\sqrt[]{105.2857} \\ S=10.26088 \end{gathered}`

By rounding the solutions to the nearest tenth, the answers are:

`\begin{gathered} \text{Range}=28 \\ \text{Variance}=105.3 \\ \text{ Standard deviation = 10.3} \end{gathered}`