Given the equations:
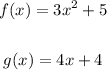
Let's find the point where both equations intersect.
To find the point let's first find the value of x by equation both expression:
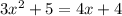
Now, equate to zero:
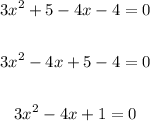
Now let's factor by grouping
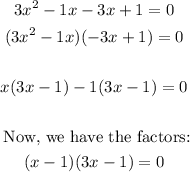
Solve each factor for x:
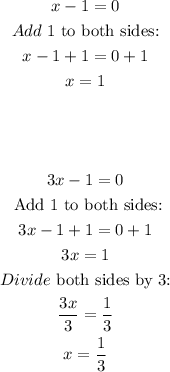
We can see from the given options, we have a point where the x-coordinate is 1 and the y-coordinate is 8.
Since we have a solution of x = 1.
Let's plug in 1 in both function and check if the result with be 8.
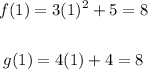
We can see the results are the same.
Therefore, the point where the two equations meet is:
(1, 8)
ANSWER:
B. (1, 8)