Question

At which of the following points do the two equations f(x)=3x^2+5 and g(x)=4x+4 intersect?A. (0,5)B. (1,8)C. (0,4) D. (8,1)

Answer 1

Given the equations:

`\begin{gathered} f(x)=3x^2+5 \\ \\ g(x)=4x+4 \end{gathered}`

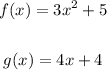
Let's find the point where both equations intersect.

To find the point let's first find the value of x by equation both expression:

`3x^2+5=4x+4`

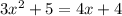
Now, equate to zero:

`\begin{gathered} 3x^2+5-4x-4=0 \\ \\ 3x^2-4x+5-4=0 \\ \\ 3x^2-4x+1=0 \end{gathered}`

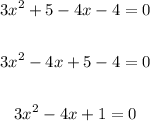
Now let's factor by grouping

`\begin{gathered} 3x^2-1x-3x+1=0 \\ (3x^2-1x)(-3x+1)=0 \\ \\ x(3x-1)-1(3x-1)=0 \\ \\ \text{ Now, we have the factors:} \\ (x-1)(3x-1)=0 \end{gathered}`

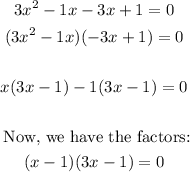
Solve each factor for x:

`\begin{gathered} x-1=0 \\ Add\text{ 1 to both sides:} \\ x-1+1=0+1 \\ x=1 \\ \\ \\ \\ 3x-1=0 \\ \text{ Add 1 to both sides:} \\ 3x-1+1=0+1 \\ 3x=1 \\ Divide\text{ both sides by 3:} \\ (3x)/(3)=(1)/(3) \\ x=(1)/(3) \end{gathered}`

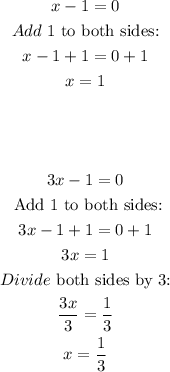
We can see from the given options, we have a point where the x-coordinate is 1 and the y-coordinate is 8.

Since we have a solution of x = 1.

Let's plug in 1 in both function and check if the result with be 8.

`\begin{gathered} f(1)=3(1)^2+5=8 \\ \\ g(1)=4(1)+4=8 \end{gathered}`

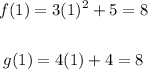
We can see the results are the same.

Therefore, the point where the two equations meet is:

(1, 8)

ANSWER:

B. (1, 8)