Question

For each quadratic expression below, drag an equivalent expression to its match

Answer 1

1. Given the expression:

`\mleft(x+2\mright)\mleft(x-4\mright)`

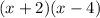
You can use the FOIL method to multiply the binomials. Remember that the FOIL method is:

`(a+b)\mleft(c+d\mright)=ac+ad+bc+bd`

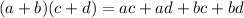
Then, you get:

`\begin{gathered} =(x)(x)-(x)(4)+(2)(x)-(2)(4) \\ =x^2-4x+2x^{}-8 \end{gathered}`

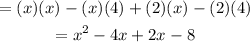
Adding the like terms, you get:

`=x^2-2x-8`

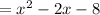
2. Given:

`x^2-6x+5`

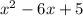
You have to complete the square:

- Identify the coefficient of the x-term". In this case, this is -6.

- Divide -6 by 2 and square the result:

`((-6)/(2))^2=(-3)^2=9`

- Now add 9 to the polynomial and also subtract 9 from the polynomial:

`=x^2-6x+(9)+5-(9)`

- Finally, simplifying and completing the square, you get:

`=(x-3)^2-4`

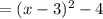
3. Given the expression:

`\mleft(x+3\mright)^2-7`

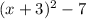
You can simplify it as follows:

- Apply:

`(a+b)^2=a^2+2ab+b^2`

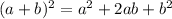
In this case:

`\begin{gathered} a=x \\ b=3 \end{gathered}`

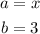
Then:

`\begin{gathered} =\lbrack(x)^2+(2)(x)(3)+(3)^2\rbrack-7 \\ =\lbrack x^2+6x+9\rbrack-7 \end{gathered}`

- Adding the like terms, you get:

`=x^2+6x+2`

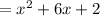
4. Given:

`x^2-8x+15`

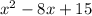
You need to complete the square by following the procedure used in expression 2.

In this case, the coefficient of the x-term is:

`b=-8`

Then:

`((-8)/(2))^2=(-4)^2=16`

By Completing the square, you get:

`\begin{gathered} =x^2-8x+(16)+15-(16) \\ =(x-4)^2-1 \end{gathered}`

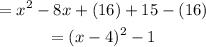
Therefore, the answer is: