1. Given the expression:
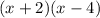
You can use the FOIL method to multiply the binomials. Remember that the FOIL method is:
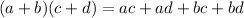
Then, you get:
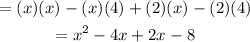
Adding the like terms, you get:
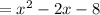
2. Given:
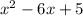
You have to complete the square:
- Identify the coefficient of the x-term". In this case, this is -6.
- Divide -6 by 2 and square the result:
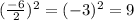
- Now add 9 to the polynomial and also subtract 9 from the polynomial:
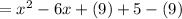
- Finally, simplifying and completing the square, you get:
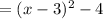
3. Given the expression:
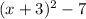
You can simplify it as follows:
- Apply:
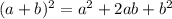
In this case:
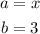
Then:
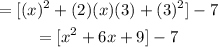
- Adding the like terms, you get:
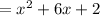
4. Given:
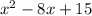
You need to complete the square by following the procedure used in expression 2.
In this case, the coefficient of the x-term is:
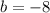
Then:
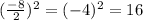
By Completing the square, you get:
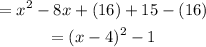
Therefore, the answer is: