Question

For the parabola given by 4y – 9 = x2 – 6x, find the vertex and focus.

Answer 1

Gievn the equation below

`4y-9=x^2-6x`

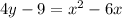
To find the vertex and focus of the given equation, we apply the parabola standard equation which is

`4p(y-k)=(x-h)^2`

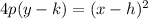
Where p is the focal length and the vertex is (h,k)

Rewriting the equation in standard form gives

`\begin{gathered} 4y-9=x^2-6x \\ 4y=x^2-6x+9 \\ 4y=x^2-3x-3x+9 \\ 4y=x(x-3)-3(x-3) \\ 4y=(x-3)^2 \\ 4(1)(y-0)=(x-3)^2 \end{gathered}`

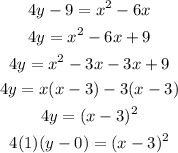
Relating the parabola standard equation with the given equation, the vertex of the parabola is

`\begin{gathered} x-3=0 \\ x=3 \\ y-0=0 \\ y=0 \\ (h,k)\Rightarrow(3,0) \\ p=1 \end{gathered}`

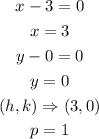
Hence, the vertex is (3,0)

The focus of the parabola formula is

`(h,k+p)`

Where

`\begin{gathered} h=3 \\ k=0 \\ p=1 \end{gathered}`

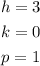
Substitute the values of h, k and p into the focus formula

`(h,k+p)\Rightarrow(3,0+1)\Rightarrow(3,1)`

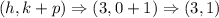
Hence, the focus is (3, 1)